[solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

 [solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

time limit per test

5 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

 [solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

In computer networks, the Internet Protocol (IP) uses path routing. With path routing, the packet contains only the destination address; routers decide which "next hop" to forward each packet on to get it closer to its destination. Each router makes this decision locally, based only on the destination address and its local configuration. One way to store this configuration is to use routing tables, which means for each router, we store the "next hop" for every possible destination. However, as the scale of the network grows larger, the size of the router table grows as well. It is a big issue since routers only have limited computing resources. One way to address this issue is to divide the graph into several partitions.

For example, in the above figure, there are 12$12$ routers in the network. Each edge has a certain weight. Each router has to store 12$12$ table entries for all possible destinations in the network (including itself). We can merge four nodes in the graph into one large abstract node R2$R2$. When routers are merged, all existing edges connected to the elements of a large node are preserved. Then all routers outside R2$R2$ only need to store 9$9$ table entries. Therefore, in this case, we can assign the same "next hop" for all destination routers in R2$R2$. The intuition behind this is that router R1$R1$ does not need to care how to get R24$R24$ from R21$R21$ if R1$R1$ wants to send a packet to R24$R24$. R1$R1$ just needs to find a path to get its packet to an arbitrary router inside R2$R2$ and then let the routers inside R2$R2$ decide how to get R24$R24$. For routers inside R2$R2$, however, there are still 12$12$ table entries, because they need to know the routes to each other.

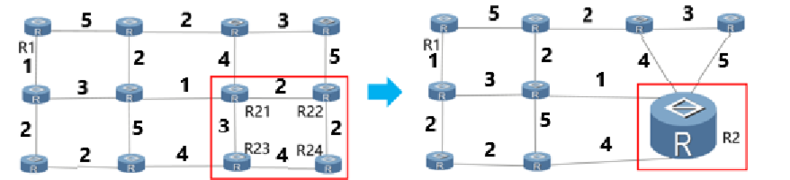
We can further merge R31,R32,R33,R34$R31,R32,R33,R34$ into a single node R3$R3$. Then for R1$R1$, we need to store only 6$6$ entries in its routing table. For routers in R3$R3$ or R2$R2$, it only needs to store 9$9$ entries. Your task is to find an optimal partition of the initial graph to minimize the maximum size of the routing table for all routers in the network.

A computer network under consideration is an undirected connected graph G=(V,E)$G=(V,E)$, where |V|=N (2≤N≤105)$|V|=N(2\le N\le {10}^5)$, |E|=M (N−1≤M≤2×105)$|E|=M(N-1\le M\le 2\times {10}^5)$, V={1,2,…,N}$V=\{1,2,\dots ,N\}$, E={e=(u,v,w)∣There is an edge between nodes u and v with weight w}.$E=\{e=(u,v,w)\mid \text{There is an edge between nodes }u\text{ and }v\text{ with weight }w\}.$

A partition P$P$ of the network G$G$ is a set of non-empty subsets of V$V$ such that every node v∈V$v\in V$ belongs to exactly one of these subsets, and the induced sub-graph for each subset in P$P$ is connected. Here, one subset corresponds to one abstract node mentioned above.

 [solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

Formally, P$P$ is a valid partition if and only if P$P$ is a family of sets that satisfies:

• ∅∉P$\mathrm{\varnothing }\notin P$
• ⋃A∈PA=V$\bigcup _{A\in P}A=V$
• ∀A,B∈P:A≠B⟹A∩B=∅$\mathrm{\forall }A,B\in P:A\ne B⟹A\cap B=\mathrm{\varnothing }$
• ∀A∈P$\mathrm{\forall }A\in P$, the induced subgraph G[A]$G[A]$ is connected

The routing table size of any node v$v$ for the corresponding partition P$P$ is defined by the following equation:

RTsize(v,P)=|P|+|Q|−1,$$RTsize(v,P)=|P|+|Q|-1,$$

where |P|$|P|$ is the number of subsets in P$P$, Q$Q$ is the subset in P$P$ such that v∈Q$v\in Q$. |Q|$|Q|$ is the size of Q$Q$.

The "next hop" is defined by the shortest path tree. For each node pair (u,v),u∈V,v∈V$(u,v),u\in V,v\in V$, the "next hop" is a node z∈V$z\in V$, such that there is an edge e∈E$e\in E$ connected from u$u$ to z$z$ directly, and dist(u,v)=w(e)+dist(z,v)$dist(u,v)=w(e)+dist(z,v)$, here dist(u,v)$dist(u,v)$ denotes the length of the shortest path from u$u$ to v$v$, and w(e)$w(e)$ denotes the weight of the edge connecting u$u$ and z$z$. The valid "next hop" may not be unique. After the graph partitioning, the "next hop" for nodes in the same subset A∈P$A\in P$ is calculated via the shortest path in the induced sub-graph G[A]$G[A]$ using the same method above. We compute the "next hop" for two nodes from different subsets of P$P$ by calculating the shortest path in the "compressed" graph (we compress all nodes in the same subset into a single node). The new graph only contains edges between nodes from different subsets. And then find the shortest path from the subset containing u$u$ to the subset containing v$v$. Suppose the first edge in this path is between (x,y)$(x,y)$. From the definition, x$x$, y$y$ are in different subsets of P$P$, and u$u$ is in the same subset of x$x$. If x=u$x=u$, then the "next hop" of (u,v)$(u,v)$ is y$y$, otherwise the "next hop" of (u,v)$(u,v)$ is the "next hop" of (u,x)$(u,x)$.

The path from u$u$ to v$v$ may differ from the path in the graph before partition.

For example:

Originally, the packet transmission path from 1$1$ to 2$2$ is the shortest in the whole graph, so it is 1→3→2$1\to 3\to 2$, and the total length is 3.

If our partition P={{1,2},{3},{4}}$P=\{\{1,2\},\{3\},\{4\}\}$, then the packet transmission path from 1$1$ to 2$2$ is the shortest path in the subgraph, so it is 1→2$1\to 2$. The total length is 10$10$, which gets much greater after partition.

Define dist(u,v)$dist(u,v)$ as the length of the shortest path from u$u$ to v$v$ in graph G$G$.

Let cost(u,v,P)$cost(u,v,P)$ be the length of the optimal transmission path after dividing graph G$G$ by partition P$P$. The way to determine cost(u,v,P)$cost(u,v,P)$ is specified later.

For node u$u$, we define B(u,P)=Q$B(u,P)=Q$, where Q$Q$ is the unique subset in P$P$ such that u∈Q$u\in Q$.

 [solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

Define two new edge sets:

EdgeZero(P)={(u,v,w)∣(u,v,w)∈E∧B(u,P)≠B(v,P)}∪{(u,v,0)∣(u,v,w)∈E∧B(u,P)=B(v,P)}$$EdgeZero(P)=\{(u,v,w)\mid (u,v,w)\in E\wedge B(u,P)\ne B(v,P)\}\cup \{(u,v,0)\mid (u,v,w)\in E\wedge B(u,P)=B(v,P)\}$$

EdgeInf(P)={(u,v,∞)∣(u,v,w)∈E∧B(u,P)≠B(v,P)}∪{(u,v,w)∣(u,v,w)∈E∧B(u,P)=B(v,P)}$$EdgeInf(P)=\{(u,v,\mathrm{\infty })\mid (u,v,w)\in E\wedge B(u,P)\ne B(v,P)\}\cup \{(u,v,w)\mid (u,v,w)\in E\wedge B(u,P)=B(v,P)\}$$

Define two undirected weighted graphs: GraphZero(P)=(V,EdgeZero(P))$GraphZero(P)=(V,EdgeZero(P))$, GraphInf(P)=(V,EdgeInf(P))$GraphInf(P)=(V,EdgeInf(P))$.

 [solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

In other words, GraphZero(P)=(V,EdgeZero(P))$GraphZero(P)=(V,EdgeZero(P))$ is almost a copy of the original graph, except for all edges that have both endpoints in the same subset of P$P$ (their weights are set to 0$0$). GraphInf(P)=(V,EdgeInf(P))$GraphInf(P)=(V,EdgeInf(P))$ is also almost a copy of the original graph, except for all edges that connect different subsets of P$P$ (their weights are set to infinity).

Let disZero(u,v,P)$disZero(u,v,P)$ be the length of the shortest path from u$u$ to v$v$ in GraphZero(P)$GraphZero(P)$.

Let disInf(u,v,P)$disInf(u,v,P)$ be the length of the shortest path from u$u$ to v$v$ in GraphInf(P)$GraphInf(P)$.

For nodes u,v: (B(u,P)≠B(v,P))$u,v:(B(u,P)\ne B(v,P))$, we define that middle(u,v,P)$middle(u,v,P)$ be the edge e=(x,y,w)∈EdgeZero(P)$e=(x,y,w)\in EdgeZero(P)$ with the smallest edge index which makes the following equation holds:

disZero(u,v,P)=disZero(u,x,P)+w+disZero(y,v,P), w>0$$disZero(u,v,P)=disZero(u,x,P)+w+disZero(y,v,P),w>0$$

We can prove such an edge always exists.

Then cost(u,v,P)$cost(u,v,P)$ can be calculated recursively:

• For nodes u,v: (B(u,P)=B(v,P))$u,v:(B(u,P)=B(v,P))$, cost(u,v,P)=disInf(u,v,P)$cost(u,v,P)=disInf(u,v,P)$.
• For nodes u,v: (B(u,P)≠B(v,P))$u,v:(B(u,P)\ne B(v,P))$, let e=(x,y,w)=middle(u,v,P)$e=(x,y,w)=middle(u,v,P)$, then cost(u,v,P)=cost(u,x,P)+w+cost(y,v,P)$cost(u,v,P)=cost(u,x,P)+w+cost(y,v,P)$.

Given a real number k≥0$k\ge 0$, and a vertex set S⊆V, 1≤|S|≤min(50,N)$S\subseteq V,1\le |S|\le min(50,N)$, find an optimal partition P$P$, which maximizes Score2(P)$Score2(P)$.

The score for SubTask2 for the ith$i^{th}$ graph is calculated by the formula:

Score2i=Score2(P=P(Gi))=max{0,N−[maxv∈VRTsize(v,P)]−kmaxu∈S,v∈V,u≠vcost(u,v,P)−dist(u,v)dist(u,v)}.$$Score{2}_i=Score2(P=P(G_i))=max\{0,N-[\underset{v\in V}{max}RTsize(v,P)]-k\underset{u\in S,v\in V,u\ne v}{max}\frac{cost(u,v,P)-dist(u,v)}{dist(u,v)}\}.$$

The final score for SubTask2 is calculated according to the following formula:

Score2=∑0.7×Score2i$$Score2=\sum 0.7\times Score{2}_i$$

 [solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

Input

The first line contains two integers N$N$ and M$M$ (2≤N≤105;N−1≤M≤2×105)$(2\le N\le {10}^5;N-1\le M\le 2\times {10}^5)$ — the number of nodes and edges, respectively.

Each of the next M$M$ lines contains three integers ui,vi$u_i,v_i$ and wi$w_i$ (0≤ui, vi≤N−1, ui≠vi, 1≤wi≤105$0\le u_i,v_i\le N-1,u_i\ne v_i,1\le w_i\le {10}^5$), denoting an edge between the node ui$u_i$ and vi$v_i$ with weight wi$w_i$. ei=(ui,vi,wi)$e_i=(u_i,v_i,w_i)$ is the edge with index i$i$ in the edge set E$E$. It is guaranteed that the input graph is connected and there are no multiple edges. That is, any pair (in any order) of nodes appear in this list no more than once.

The next line contains two numbers: one integer SetSize$SetSize$ (1≤SetSize≤min(50,N)$1\le SetSize\le min(50,N)$), the size of node set S$S$ and one real number k$k$, given with at most six digits after the decimal point (0≤k≤106)$(0\le k\le {10}^6)$.

Each of the next SetSize$SetSize$ lines contains one integer NodeID$NodeID$ (0≤NodeID≤N−1$0\le NodeID\le N-1$), the node in S$S$.

 [solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

Output

In the first line, output the number of subsets in your partition P$P$.

The (i+1)$(i+1)$-th line should begin with a single number cnti$cn{t}_i$ — the size of the i$i$-th subset, followed by cnti$cn{t}_i$ numbers, denoting the node IDs in the i$i$-th subset.

 [solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

Scoring

During the coding phase, your solutions are tested against pre-tests only. The first 6$6$ of them are open and available for download at the link problem-gp2-open-testset.zip in the "contest materials" section in a sidebar.

After the end of the coding phase, the last submission that scored a positive number of points on the pre-tests will be selected. It will be retested in the final tests. The rest of your submissions will be ignored. The final tests are secret and not available to the participants, they are mostly realistic. The result obtained on the final tests is your final official result for this problem.

1. According to the formula, the solution with a larger score wins.
2. If two solutions have the same score, the solution submitted first wins.
3. For multiple test cases, the ranking is performed based on the following formula:
   Score2=∑0.7×Score2i.$$Score2=\sum 0.7\times Score{2}_i.$$
4. Final formula for the "ICPC 2022 Online Challenge powered by HUAWEI - Problem 1":
   FinalScore=Score1+Score2.$$FinalScore=Score1+Score2.$$

 [solution] GP2. Optimal Graph Partition for Fast Routing (GP2)

Examples

input

Copy

4 4
0 1 10
2 3 12
0 2 2
2 1 1
4 0
0
1
2
3

output

Copy

2
2 0 1
2 2 3

input

Copy

4 4
0 1 10
2 3 12
0 2 2
2 1 1
4 2.3
0
1
2
3

output

Copy

2
2 0 1
2 2 3