Codeforces Round #827 (Div. 4)

Codeforces Round #827 (Div. 4)

A. Sum

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given three integers a$a$, b$b$, and c$c$. Determine if one of them is the sum of the other two.

Input

The first line contains a single integer t$t$ (1≤t≤9261$1\le t\le 9261$) — the number of test cases.

The description of each test case consists of three integers a$a$, b$b$, c$c$ (0≤a,b,c≤20$0\le a,b,c\le 20$).

Output

For each test case, output "YES" if one of the numbers is the sum of the other two, and "NO" otherwise.

You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).

Example

input

Copy

7
1 4 3
2 5 8
9 11 20
0 0 0
20 20 20
4 12 3
15 7 8

output

Copy

YES
NO
YES
YES
NO
NO
YES

Note

In the first test case, 1+3=4$1+3=4$.

In the second test case, none of the numbers is the sum of the other two.

In the third test case, 9+11=20$9+11=20$.

B. Increasing

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an array a$a$ of n$n$ positive integers. Determine if, by rearranging the elements, you can make the array strictly increasing. In other words, determine if it is possible to rearrange the elements such that a1<a2<⋯<an$a_1<a_2<\cdots <a_n$ holds.

Input

The first line contains a single integer t$t$ (1≤t≤100$1\le t\le 100$) — the number of test cases.

The first line of each test case contains a single integer n$n$ (1≤n≤100$1\le n\le 100$) — the length of the array.

The second line of each test case contains n$n$ integers ai$a_i$ (1≤ai≤109$1\le a_i\le {10}^9$) — the elements of the array.

Output

For each test case, output "YES" (without quotes) if the array satisfies the condition, and "NO" (without quotes) otherwise.

You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).

Example

input

Copy

3
4
1 1 1 1
5
8 7 1 3 4
1
5

output

Copy

NO
YES
YES

Note

In the first test case any rearrangement will keep the array [1,1,1,1]$[1,1,1,1]$, which is not strictly increasing.

In the second test case, you can make the array [1,3,4,7,8]$[1,3,4,7,8]$.

C. Stripes

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

On an 8×8$8\times 8$ grid, some horizontal rows have been painted red, and some vertical columns have been painted blue, in some order. The stripes are drawn sequentially, one after the other. When the stripe is drawn, it repaints all the cells through which it passes.

Determine which color was used last.

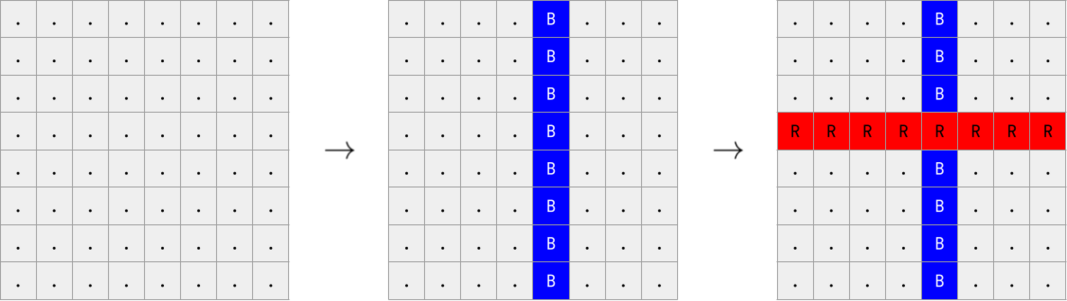The red stripe was painted after the blue one, so the answer is R.

Input

The first line of the input contains a single integer t$t$ (1≤t≤4000$1\le t\le 4000$) — the number of test cases. The description of test cases follows. There is an empty line before each test case.

Each test case consists of 8$8$ lines, each containing 8$8$ characters. Each of these characters is either 'R', 'B', or '.', denoting a red square, a blue square, and an unpainted square, respectively.

It is guaranteed that the given field is obtained from a colorless one by drawing horizontal red rows and vertical blue columns.

At least one stripe is painted.

Output

For each test case, output 'R' if a red stripe was painted last, and 'B' if a blue stripe was painted last (without quotes).

Example

input

Copy

4

....B...
....B...
....B...
RRRRRRRR
....B...
....B...
....B...
....B...

RRRRRRRB
B......B
B......B
B......B
B......B
B......B
B......B
RRRRRRRB

RRRRRRBB
.B.B..BB
RRRRRRBB
.B.B..BB
.B.B..BB
RRRRRRBB
.B.B..BB
.B.B..BB

........
........
........
RRRRRRRR
........
........
........
........

output

Copy

R
B
B
R

Note

The first test case is pictured in the statement.

In the second test case, the first blue column is painted first, then the first and last red rows, and finally the last blue column. Since a blue stripe is painted last, the answer is B.

D. Coprime

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Given an array of n$n$ positive integers a1,a2,…,an$a_1,a_2,\dots ,a_n$ (1≤ai≤1000$1\le a_i\le 1000$). Find the maximum value of i+j$i+j$ such that ai$a_i$ and aj$a_j$ are coprime,†${}^{†}$ or −1$-1$ if no such i$i$, j$j$ exist.

For example consider the array [1,3,5,2,4,7,7]$[1,3,5,2,4,7,7]$. The maximum value of i+j$i+j$ that can be obtained is 5+7$5+7$, since a5=4$a_5=4$ and a7=7$a_7=7$ are coprime.

†${}^{†}$ Two integers p$p$ and q$q$ are coprime if the only positive integer that is a divisor of both of them is 1$1$ (that is, their greatest common divisor is 1$1$).

Input

The input consists of multiple test cases. The first line contains an integer t$t$ (1≤t≤10$1\le t\le 10$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains an integer n$n$ (2≤n≤2⋅105$2\le n\le 2\cdot {10}^5$) — the length of the array.

The following line contains n$n$ space-separated positive integers a1$a_1$, a2$a_2$,..., an$a_n$ (1≤ai≤1000$1\le a_i\le 1000$) — the elements of the array.

It is guaranteed that the sum of n$n$ over all test cases does not exceed 2⋅105$2\cdot {10}^5$.

Output

For each test case, output a single integer  — the maximum value of i+j$i+j$ such that i$i$ and j$j$ satisfy the condition that ai$a_i$ and aj$a_j$ are coprime, or output −1$-1$ in case no i$i$, j$j$ satisfy the condition.

Example

input

Copy

6
3
3 2 1
7
1 3 5 2 4 7 7
5
1 2 3 4 5
3
2 2 4
6
5 4 3 15 12 16
5
1 2 2 3 6

output

Copy

6
12
9
-1
10
7

Note

For the first test case, we can choose i=j=3$i=j=3$, with sum of indices equal to 6$6$, since 1$1$ and 1$1$ are coprime.

For the second test case, we can choose i=7$i=7$ and j=5$j=5$, with sum of indices equal to 7+5=12$7+5=12$, since 7$7$ and 4$4$ are coprime.

E. Scuza

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Timur has a stairway with n$n$ steps. The i$i$-th step is ai$a_i$ meters higher than its predecessor. The first step is a1$a_1$ meters higher than the ground, and the ground starts at 0$0$ meters.

The stairs for the first test case.

Timur has q$q$ questions, each denoted by an integer k1,…,kq$k_1,\dots ,k_q$. For each question ki$k_i$, you have to print the maximum possible height Timur can achieve by climbing the steps if his legs are of length ki$k_i$. Timur can only climb the j$j$-th step if his legs are of length at least aj$a_j$. In other words, ki≥aj$k_i\ge a_j$ for each step j$j$ climbed.

Note that you should answer each question independently.

Input

The first line contains a single integer t$t$ (1≤t≤100$1\le t\le 100$) — the number of test cases.

The first line of each test case contains two integers n,q$n,q$ (1≤n,q≤2⋅105$1\le n,q\le 2\cdot {10}^5$) — the number of steps and the number of questions, respectively.

The second line of each test case contains n$n$ integers (1≤ai≤109$1\le a_i\le {10}^9$) — the height of the steps.

The third line of each test case contains q$q$ integers (0≤ki≤109$0\le k_i\le {10}^9$) — the numbers for each question.

It is guaranteed that the sum of n$n$ does not exceed 2⋅105$2\cdot {10}^5$, and the sum of q$q$ does not exceed 2⋅105$2\cdot {10}^5$.

Output

For each test case, output a single line containing q$q$ integers, the answer for each question.

Please note, that the answer for some questions won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).

Example

input

Copy

3
4 5
1 2 1 5
1 2 4 9 10
2 2
1 1
0 1
3 1
1000000000 1000000000 1000000000
1000000000

output

Copy

1 4 4 9 9 
0 2 
3000000000 

Note

Consider the first test case, pictured in the statement.

• If Timur's legs have length 1$1$, then he can only climb stair 1$1$, so the highest he can reach is 1$1$ meter.
• If Timur's legs have length 2$2$ or 4$4$, then he can only climb stairs 1$1$, 2$2$, and 3$3$, so the highest he can reach is 1+2+1=4$1+2+1=4$ meters.
• If Timur's legs have length 9$9$ or 10$10$, then he can climb the whole staircase, so the highest he can reach is 1+2+1+5=9$1+2+1+5=9$ meters.

In the first question of the second test case, Timur has no legs, so he cannot go up even a single step. :(

F. Smaller

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Alperen has two strings, s$s$ and t$t$ which are both initially equal to "a".

He will perform q$q$ operations of two types on the given strings:

• 1kx$1kx$ — Append the string x$x$ exactly k$k$ times at the end of string s$s$. In other words, s:=s+x+⋯+xk times$s:=s+\underset{k\text{ times}}{\underbrace{x+\cdots +x}}$.
• 2kx$2kx$ — Append the string x$x$ exactly k$k$ times at the end of string t$t$. In other words, t:=t+x+⋯+xk times$t:=t+\underset{k\text{ times}}{\underbrace{x+\cdots +x}}$.

After each operation, determine if it is possible to rearrange the characters of s$s$ and t$t$ such that s$s$ is lexicographically smaller†${}^{†}$ than t$t$.

Note that the strings change after performing each operation and don't go back to their initial states.

†${}^{†}$ Simply speaking, the lexicographical order is the order in which words are listed in a dictionary. A formal definition is as follows: string p$p$ is lexicographically smaller than string q$q$ if there exists a position i$i$ such that pi<qi$p_i<q_i$, and for all j<i$j<i$, pj=qj$p_j=q_j$. If no such i$i$ exists, then p$p$ is lexicographically smaller than q$q$ if the length of p$p$ is less than the length of q$q$. For example, abdc<abe$\mathtt{\text{abdc}}<\mathtt{\text{abe}}$ and abc<abcd$\mathtt{\text{abc}}<\mathtt{\text{abcd}}$, where we write p<q$p<q$ if p$p$ is lexicographically smaller than q$q$.

Input

The first line of the input contains an integer t$t$ (1≤t≤104$1\le t\le {10}^4$) — the number of test cases.

The first line of each test case contains an integer q$q$ (1≤q≤105)$(1\le q\le {10}^5)$ — the number of operations Alperen will perform.

Then q$q$ lines follow, each containing two positive integers d$d$ and k$k$ (1≤d≤2$1\le d\le 2$; 1≤k≤105$1\le k\le {10}^5$) and a non-empty string x$x$ consisting of lowercase English letters — the type of the operation, the number of times we will append string x$x$ and the string we need to append respectively.

It is guaranteed that the sum of q$q$ over all test cases doesn't exceed 105${10}^5$ and that the sum of lengths of all strings x$x$ in the input doesn't exceed 5⋅105$5\cdot {10}^5$.

Output

For each operation, output "YES", if it is possible to arrange the elements in both strings in such a way that s$s$ is lexicographically smaller than t$t$ and "NO" otherwise.

Example

input

Copy

3
5
2 1 aa
1 2 a
2 3 a
1 2 b
2 3 abca
2
1 5 mihai
2 2 buiucani
3
1 5 b
2 3 a
2 4 paiu

output

Copy

YES
NO
YES
NO
YES
NO
YES
NO
NO
YES

Note

In the first test case, the strings are initially s=$s=$ "a" and t=$t=$ "a".

After the first operation the string t$t$ becomes "aaa". Since "a" is already lexicographically smaller than "aaa", the answer for this operation should be "YES".

After the second operation string s$s$ becomes "aaa", and since t$t$ is also equal to "aaa", we can't arrange s$s$ in any way such that it is lexicographically smaller than t$t$, so the answer is "NO".

After the third operation string t$t$ becomes "aaaaaa" and s$s$ is already lexicographically smaller than it so the answer is "YES".

After the fourth operation s$s$ becomes "aaabb" and there is no way to make it lexicographically smaller than "aaaaaa" so the answer is "NO".

After the fifth operation the string t$t$ becomes "aaaaaaabcaabcaabca", and we can rearrange the strings to: "bbaaa" and "caaaaaabcaabcaabaa" so that s$s$ is lexicographically smaller than t$t$, so we should answer "YES".

G. Orray

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an array a$a$ consisting of n$n$ nonnegative integers.

Let's define the prefix OR array b$b$ as the array bi=a1 OR a2 OR … OR ai$b_i=a_1\mathsf{O}\mathsf{R}{a}_2\mathsf{O}\mathsf{R}\dots \mathsf{O}\mathsf{R}{a}_i$, where OR$\mathsf{O}\mathsf{R}$ represents the bitwise OR operation. In other words, the array b$b$ is formed by computing the OR$\mathsf{O}\mathsf{R}$ of every prefix of a$a$.

You are asked to rearrange the elements of the array a$a$ in such a way that its prefix OR array is lexicographically maximum.

An array x$x$ is lexicographically greater than an array y$y$ if in the first position where x$x$ and y$y$ differ, xi>yi$x_i>y_i$.

Input

The first line of the input contains a single integer t$t$ (1≤t≤100$1\le t\le 100$) — the number of test cases. The description of test cases follows.

The first line of each test case contains a single integer n$n$ (1≤n≤2⋅105$1\le n\le 2\cdot {10}^5$) — the length of the array a$a$.

The second line of each test case contains n$n$ nonnegative integers a1,…,an$a_1,\dots ,a_n$ (0≤ai≤109$0\le a_i\le {10}^9$).

It is guaranteed that the sum of n$n$ over all test cases does not exceed 2⋅105$2\cdot {10}^5$.

Output

For each test case print n$n$ integers — any rearrangement of the array a$a$ that obtains the lexicographically maximum prefix OR array.

Example

input

Copy

5
4
1 2 4 8
7
5 1 2 3 4 5 5
2
1 101
6
2 3 4 2 3 4
8
1 4 2 3 4 5 7 1

output

Copy

8 4 2 1 
5 2 1 3 4 5 5 
101 1 
4 3 2 2 3 4 
7 1 4 2 3 4 5 1 

Codeforces