Problem Solution Dytechlab Cup 2022
Dytechlab Cup 2022
 | Ela loves reading a lot, just like her new co-workers in DTL! On her first day after becoming an engineer in DTL, she is challenged by a co-worker to sort a heap of books into different compartments on the shelf. |
books must be split into compartments on the bookshelf ( is divisible by ). Each book is represented by a lowercase Latin letter from 'a' to 'y' inclusively, which is the beginning letter in the title of the book.
Ela must stack exactly books in each compartment. After the books are stacked, for each compartment indexed from to , she takes the minimum excluded (MEX) letter of the multiset of letters formed by letters representing all books in that compartment, then combines the resulting letters into a string. The first letter of the resulting string is the MEX letter of the multiset of letters formed by the first compartment, the second letter of the resulting string is the MEX letter of the multiset of letters formed by the second compartment, ... and so on. Please note, under the constraint of this problem, MEX letter can always be determined for any multiset found in this problem because 'z' is not used.
What is the lexicographically greatest resulting string possible that Ela can create?
A string is lexicographically greater than a string if and only if one of the following holds:
- is a prefix of , but ;
- in the first position where and differ, the string has a letter that appears later in the alphabet than the corresponding letter in .
The minimum excluded (MEX) letter of a multiset of letters is the letter that appears earliest in the alphabet and is not contained in the multiset. For example, if a multiset of letters contains letters 'b', 'a', 'b', 'c', 'e', 'c', 'f' respectively, then the MEX letter of this compartment is 'd', because 'd' is not included in the multiset, and all letters comes before 'd' in the alphabet, namely 'a', 'b' and 'c', are included in the multiset.
Each test contains multiple test cases. The first line contains the number of test cases (). Description of the test cases follows.
The first line of each test case contains two integers and (; ). It is guaranteed that is divisible by .
The second line of each test case contains a string of lowercase Latin letters from 'a' to 'y' inclusively. Each letter represents the starting letter of the title of a book in the initial heap.
It is guaranteed that the sum of over all test cases does not exceed .
For each test case, output a string of letters which is the most optimal string that Ela can find.
512 3cabccadabaac12 6cabccadabaac12 12cabccadabaac25 1abcdefghijklmnopqrstuvwxy10 5bcdxedbcfg
edb
ccbbba
bbbbbaaaaaaa
z
aaaaa
In the first test case, the books can be divided into compartments as below:
- the first compartment contains the books with indices : 'c', 'a', 'b', 'd' 'e'
- the second compartment contains the books with indices : 'c', 'c', 'a', 'b' 'd'
- the third compartment contains the remaining books : 'a', 'a', 'a', 'c' 'b'
Therefore, the answer is 'edb'. It can be proven that there is no way that Ela can arrange the books so that it results in a lexicographically greater string.

 | While working at DTL, Ela is very aware of her physical and mental health. She started to practice various sports, such as Archery, Yoga, and Football. |
Since she started engaging in sports activities, Ela switches to trying a new sport on days she considers being "Luxury" days. She counts the days since she started these activities, in which the day she starts is numbered as day . A "Luxury" day is the day in which the number of this day is a luxurious number.
An integer is called a luxurious number if it is divisible by .
Here denotes the "floor" of a real number . In other words, it's the largest integer not greater than .
For example: , , are luxurious numbers, since is divisible by , is divisible , and is divisible by , respectively. On the other hand , are not, since are not divisible by , and are not divisible by .
Being a friend of Ela, you want to engage in these fitness activities with her to keep her and yourself accompanied (and have fun together, of course). Between day and day , you want to know how many times she changes the activities.
Each test contains multiple test cases. The first line has the number of test cases (). The description of the test cases follows.
The only line of each test case contains two integers and () — the intervals at which you want to know how many times Ela changes her sports.
For each test case, output an integer that denotes the answer.
58 198 20119 1211 1000000000000000001234567891011 1000000000000000000
5
6
2
948683296
2996666667
In the first test case, luxury numbers in range are: .
 | Ela likes Chess a lot. During breaks, she usually challenges her co-worker in DTL to some chess games. She's not an expert at classic chess, but she's very interested in Chess variants, where she has to adapt to new rules and test her tactical mindset to win the game. |
The problem, which involves a non-standard chess pieces type that is described below, reads: given white crickets on a board, arranged in an "L" shape next to each other, there are no other pieces on the board. Ela wants to know with a finite number of moves, can she put any white cricket on the square on row , column ?
An "L"-shape piece arrangement can only be one of the below:
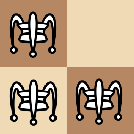 |  |
 |  |
For simplicity, we describe the rules for crickets on the board where only three white crickets are. It can move horizontally, vertically, or diagonally, but only to a square in some direction that is immediately after another cricket piece (so that it must jump over it). If the square immediately behind the piece is unoccupied, the cricket will occupy the square. Otherwise (when the square is occupied by another cricket, or does not exist), the cricket isn't allowed to make such a move.
See an example of valid crickets' moves on the pictures in the Note section.
Each test contains multiple test cases. The first line contains the number of test cases (). The description of the test cases follows.
The first line of each test case contains () — denotes the size of the chessboard.
The second line of each test case contains 6 numbers: , , , , , () — coordinates of the crickets. The input ensures that the three crickets are arranged in an "L" shape that the legend stated.
The third line of each test case contains 2 numbers: , () — coordinates of the target square.
For each test case, print "YES" or "NO" to denotes whether Ela can put a cricket on the target square.
687 2 8 2 7 15 182 2 1 2 2 15 582 2 1 2 2 16 681 1 1 2 2 15 582 2 1 2 2 18 888 8 8 7 7 84 8
YES
NO
YES
NO
YES
YES
Here's the solution for the first test case. The red square denotes where the crickets need to reach. Note that in chess horizontals are counted from bottom to top, as well as on this picture.


Ela needs to send a large package from machine to machine through a network of machines. Currently, with the network condition, she complains that the network is too slow and the package can't arrive in time. Luckily, a Wiring Wizard offered her a helping hand.
The network can be represented as an undirected connected graph with nodes, each node representing a machine. wires are used to connect them. Wire is used to connect machines and , and has a weight . The aforementioned large package, if going through wire , will move from machine to machine (or vice versa) in exactly microseconds. The Wiring Wizard can use his spell an arbitrary number of times. For each spell, he will choose the wire of index , connecting machine and , and rewire it following these steps:
- Choose one machine that is connected by this wire. Without loss of generality, let's choose .
- Choose a machine that is currently connecting to (including ), call it . Disconnect the wire indexed from , then using it to connect and .
The rewiring of wire will takes microseconds, and the weight of the wire will not change after this operation. After a rewiring, a machine might have some wire connect it with itself. Also, the Wiring Wizard has warned Ela that rewiring might cause temporary disconnections between some machines, but Ela just ignores it anyway. Her mission is to send the large package from machine to machine as fast as possible. Note that the Wizard can use his spell on a wire zero, one, or many times. To make sure the network works seamlessly while transferring the large package, once the package starts transferring from machine , the Wiring Wizard cannot use his spell to move wires around anymore.
Ela wonders, with the help of the Wiring Wizard, what is the least amount of time needed to transfer the large package from machine to .
Each test contains multiple test cases. The first line contains the number of test cases (). The description of the test cases follows.
The first line contains and (, ), the number of nodes and number of wires, respectively.
For the next lines, -th line will contains , and (, ) - the indices 2 machines that are connected by the -th edge and the weight of it.
It is guaranteed that the sum of over all test cases does not exceed and the sum of over all test cases does not exceed . The graph in each test case is guaranteed to be connected, no self-loops, but it can contain multiple edges.
For each test case, output one integer denotes the least amount of time needed to transfer the large package from machine to .
38 91 2 36 4 53 5 66 1 37 4 43 8 42 3 37 8 54 5 24 51 2 12 4 13 4 13 1 11 3 28 84 6 927 1 656 5 436 7 964 3 744 8 547 4 992 5 22
9
2
154
Here is the graph in the first test case in the sample input:
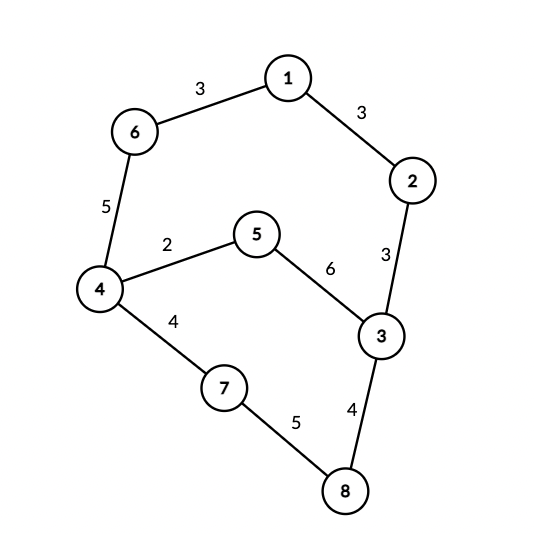
Ela can ask the Wiring Wizard to use his spell on wire with the index of , which is connecting machines and . Then, since the machine is connected to machine , the Wiring Wizard can disconnect wire from machine and connect it to machine in microseconds (weight of wire ).
After that, the package can be sent from machine to machine in microseconds. Therefore, the answer is microseconds.
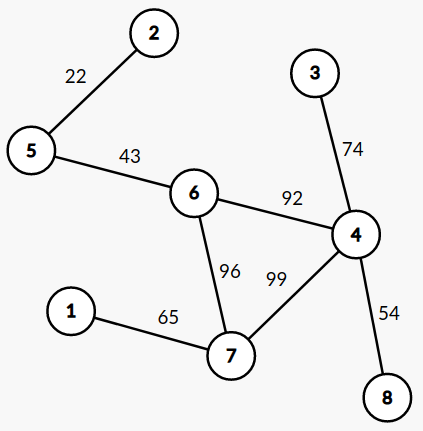
Here is the graph in the third test case in the sample input:
 | Ela likes to go hiking a lot. She loves nature and exploring the various creatures it offers. One day, she saw a strange type of ant, with a cannibalistic feature. More specifically, an ant would eat any ants that it sees which is smaller than it. Curious about this feature from a new creature, Ela ain't furious. She conducts a long, non-dubious, sentimental experiment. |
She puts cannibalistic ants in a line on a long wooden stick. Initially, the ants have the same weight of . The distance between any two consecutive ants is the same. The distance between the first ant in the line to the left end and the last ant in the line to the right end is also the same as the distance between the ants. Each ant starts moving towards the left-end or the right-end randomly and equiprobably, at the same constant pace throughout the experiment. Two ants will crash if they are standing next to each other in the line and moving in opposite directions, and ants will change direction immediately when they reach the end of the stick. Ela can't determine the moving direction of each ant, but she understands very well their behavior when crashes happen.
- If a crash happens between two ants of different weights, the heavier one will eat the lighter one, and gain the weight of the lighter one. After that, the heavier and will continue walking in the same direction. In other words, if the heavier one has weight and walking to the right, the lighter one has weight and walking to the left (), then after the crash, the lighter one will diminish, and the heavier one will have weight and continue walking to the right.
- If a crash happens between two ants with the same weight, the one walking to the left end of the stick will eat the one walking to the right, and then continue walking in the same direction. In other words, if one ant of weight walking to the left, crashes with another ant of weight walking to the right, the one walking to the right will disappear, and the one walking to the left will have to weight and continue walking to the left.
Please, check the example in the "Note" section, which will demonstrate the ants' behavior as above.
We can prove that after a definite amount of time, there will be only one last ant standing. Initially, each ant can randomly and equiprobably move to the left or the right, which generates different cases of initial movements for the whole pack. For each position in the line, calculate the probability that the ant begins in that position and survives. Output it modulo .
Formally, let . It can be shown that the answer can be expressed as an irreducible fraction , where and are integers and . Output the integer equal to . In other words, output such an integer that and .
Each test contains multiple test cases. The first line contains the number of test cases (). The description of the test cases follows.
The only line of each test contains an integer () — the number of ants in the experiment.
It is guaranteed that the sum of in all tests will not exceed .
For each test, print lines. -th line contains a single number that denotes the survival probability of the -th ant in the line modulo .
3452
0
250000002
250000002
500000004
0
250000002
250000002
250000002
250000002
0
1
Here is the example of ants moving on the branch. An ant's movement will be denoted by either a character or . Initially, the pack of ants on the branch will move as . Here's how the behavior of the pack demonstrated:

Initially, the ants are positioned as above.

After a while, the ant with index (walking to the left) will crash with the ant with index (walking to the right). The two ants have the same weight, therefore, ant will eat ant and gain its weight to . The same thing happens with ant and ant .
The ant will walk to the end of the stick, therefore changing its direction.

After that, the ant with index will crash with the ant with index . Since ant is more heavy (weight=) than ant (weight=), ant will eat ant and gain its weight to .
Ant will walk to the end of the stick, therefore changing its direction.
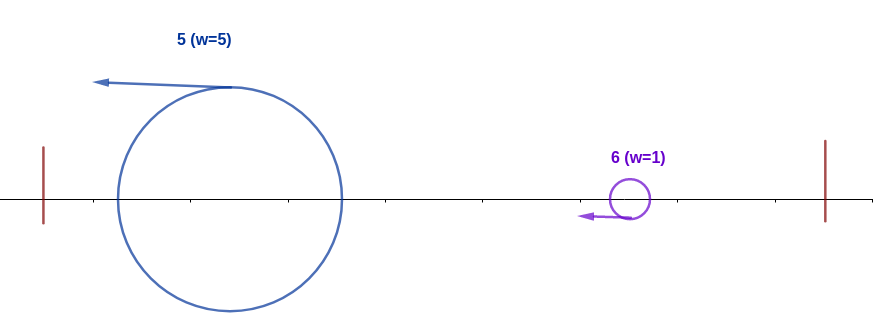
After that, the ant with index will crash with the ant with index . Since ant is more heavy (weight=) than ant (weight=), ant will eat ant and gain its weight to .
Lastly, after ant walk to the end of the branch and changes its direction, ant will eat ant and be the last ant standing.
 | After a long, tough, but fruitful day at DTL, Ela goes home happily. She entertains herself by solving Competitive Programming problems. She prefers short statements, because she already read too many long papers and documentation at work. The problem of the day reads: |
You are given an integer . Suppose that has divisors. You have to find a sequence with integers , which satisfies the following conditions:
- Each element is strictly greater than .
- Each element is a divisor of .
- All elements are distinct.
- For all , is a prime number.
In this problem, because can be too big, the result of prime factorization of is given instead. Note that denotes the greatest common divisor (GCD) of integers and and a prime number is a positive integer which has exactly divisors.
The first line contains one integer () - the number of test cases.
The first line of each test case contains one integer () - the number of prime factor of .
The second line of each test case contains integers () — exponents of corresponding prime factors of , so that and hold. is the -th smallest prime number.
It is guaranteed that the sum of over all test cases does not exceed .
Print the answer for each test case, one per line. If there is no sequence for the given , print .
Otherwise, print lines. In -th line, print space-separated integers. The -th integer of -th line is equal to the exponent of -th prime number from .
If there are multiple answers, print any of them.
521 11131 1 11422 1
0 1
1 1
1 0
1
0 1 1
0 0 1
1 0 1
1 1 0
0 1 0
1 1 1
1 0 0
-1
2 0
1 1
0 1
2 1
1 0
In each test case, the values of are , , , , and in that order.
In the first test case, , , , are divisors of . Here, sequences and can be answer. Permutation is invalid because is not a prime number.
In the forth test case, , , , , are divisors of . Among the permutation of sequence , no valid answer exist.
 | DTL engineers love partying in the weekend. Ela does, too! Unfortunately, she didn't know how to dance yet. Therefore, she decided to take a dancing class. |
There are students in the dancing class, including Ela. In the final project, students will participate in a choreography described below.
students are positioned on the positive side of the -axis. The -th dancer is located at . Some dancers will change positions during the dance (we'll call them movable dancers), and others will stay in the same place during a choreography (we'll call them immovable dancers). We distinguish the dancers using a binary string of length : if equals '1', then the -th dancer is movable, otherwise the -th dancer is immovable.
Let's call the "positive energy value" of the choreography . The dancers will perform "movements" based on this value.
Each minute after the dance begins, the movable dancer with the smallest -coordinate will start moving to the right and initiate a "movement". At the beginning of the movement, the dancer's energy level will be initiated equally to the positive energy value of the choreography, which is . Each time they move from some to , the energy level will be decreased by . At some point, the dancer might meet other fellow dancers in the same coordinates. If it happens, then the energy level of the dancer will be increased by . A dancer will stop moving to the right when his energy level reaches , and he doesn't share a position with another dancer.
The dancers are very well-trained, and each "movement" will end before the next minute begins.
To show her understanding of this choreography, Ela has to answer queries, each consisting of two integers and . The answer to this query is the coordinate of the -th dancer of both types from the left at -th minute after the choreography begins. In other words, denote as the sorted coordinates of the dancers at -th minute from the beginning, you need to print .
The first line contains three integers , and (; ; ) — the number of dancers, the positive energy value of the choreography, and the number of queries.
The second line contains integers () — the coordinates of each dancer.
The third line contains a binary string of length — the movability of each dancer. Each character is either '0' or '1'. It is guaranteed that contains at least one character '1'.
Then lines follow, the -th of them contains two integers and (, ) — the content of each query.
Output lines, each contains a single integer — the answer for the corresponding query.
4 3 8
1 3 6 7
1011
1 1
1 2
1 3
1 4
2 1
2 2
2 3
2 4
3
5
6
7
3
6
7
10
1 1 5
2
1
1 1
2 1
3 1
4 1
5 1
3
4
5
6
7
Let's consider the first example test case.
In the first minute, is the lowest coordinate between movable dancers. The energy level is initiated with . Then the following happens:
- The dancer moves from to . The energy level decreased to .
- The dancer moves from to . The energy level decreased to , then increased to when she met another dancer at .
- The dancer moves from to . The energy level decreased to .
- The dancer moves from to . The energy level decreased to .
At the end of the first minute, the sorted coordinates of the dancers become , and their respective movability is '0111'.
In the second minute, is the lowest coordinate between movable dancers. The energy level is initiated with . Then the following happens:
- The dancer moves from to . The energy level decreased to , then increased to when she met another dancer at .
- The dancer moves from to . The energy level decreased to , then increased to when she met another dancer at .
- The dancer moves from to . The energy level decreased to .
- The dancer moves from to . The energy level decreased to .
- The dancer moves from to . The energy level decreased to .
At the end of the second minute, the sorted coordinates of the dancers become , and their respective movability is '0111'.

Comments
Post a Comment